วันอังคารที่ผ่านมาผมไปทำกิจกรรมวิทยาศาสตร์กับเด็กๆมาครับ เด็กประถมต้นได้เรียนรู้เพิ่มเรื่องการสมดุลและได้ทำของเล่นสมดุลที่เป็นนกที่ทรงตัวอยู่ได้แบบประหลาดๆ เด็กประถมปลายเริ่มเรียนรู้เรื่องการเติบโตแบบเอ็กซ์โปเนนเชียลโดยลองประมาณจำนวนเซลล์ที่แบ่งตัวหลายๆรอบ (ต่อยอดมาจากความฝืดของเชือกที่เพิ่มแบบเอ็กซ์โปเนนเชียลตามจำนวนรอบพันหลักเมื่อสัปดาห์ที่แล้ว) เด็กอนุบาลสามได้เล่นลูกแก้วในกาละมังเพื่อให้เริ่มชินกับการเคลื่อนที่เป็นวงกลมครับ

(อัลบั้มบรรยากาศกิจกรรมอยู่ที่นี่นะครับ กิจกรรมคราวที่แล้วเรื่อง “ดูคลิปเคลื่อนไหวประหลาด จุดศูนย์ถ่วง ความฝืดของเชือกพันหลัก” ครับ)

สำหรับเด็กประถมต้นเราคุยกันต่อเรื่องจุดศูนย์ถ่วงครับ ผมเอาไม้บรรทัดมาถ่วงด้วยน็อตจำนวนต่างๆกันที่ตำแหน่งต่างๆกันให้เด็กๆเดาว่าจะเกิดอะไรขึ้น เด็กๆได้สังเกตจุดหมุน ระยะทางระหว่างจุดหมุนถึงน้ำหนักถ่วง และเห็นว่าถ้าจะถ่วงให้สมดุลน้ำหนักที่มากต้องอยู่ใกล้จุดหมุนขณะที่อีกข้างหนึ่งน้ำหนักเบาต้องอยู่ห่างๆจุดหมุนครับ หน้าตาการทดลองเป็นแบบนี้:

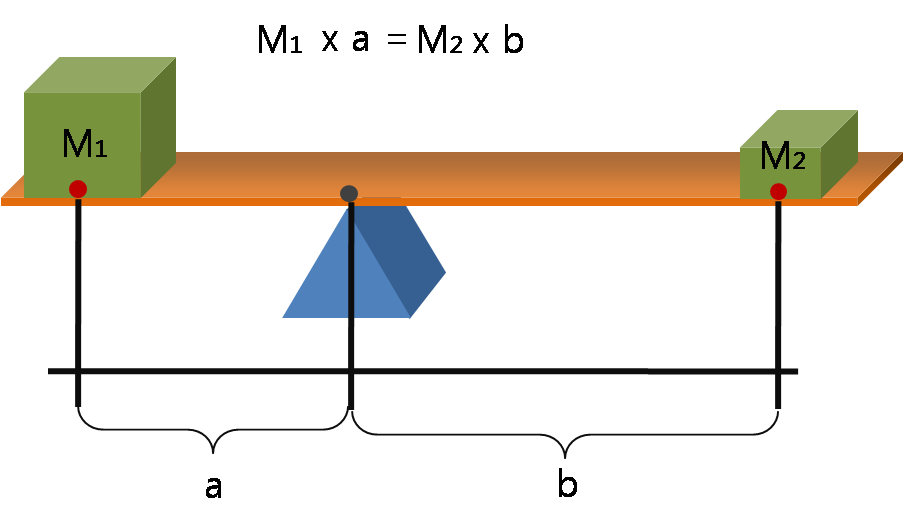
อาร์คิมีดีสค้นพบความสัมพันธ์ระหว่างน้ำหนักถ่วงทั้งสองข้างและระยะทางจากน้ำหนักถ่วงทั้งสองถึงจุดหมุนไว้เมื่อสองพันกว่าปีที่แล้วครับว่าถ้าให้ของที่ถ่วงสองข้างมีน้ำหนัก(หรือมวล ซึ่งแปรผันตรงกับน้ำหนัก) เป็น M1 และ M2 และระยะทางถึงจุดหมุนคือ a และ b ความสมดุลจะเกิดได้เมื่อ M1 x a = M2 x b ครับ

หลังจากนั้นผมก็สอนเด็กๆทำของเล่น “นกลอย” ครับ วิธีทำตามคลิปนี้ครับ:

 แล้วเด็กๆก็แยกย้ายกันทำและเล่นของเล่นครับ:

สำหรับเด็กประถมปลายผมต่อยอดเรื่องการเติบโตแบบเรขาคณิตหรือการเติบโตแบบเอ็กซ์โปเนนเชียลครับ สืบเนื่องมาจากการทดลองสัปดาห์ที่แล้วที่การเพิ่มของความฝืดที่เติบโตแบบนั้นเมื่อจำนวนรอบพันหลักเพิ่มขึ้น คือทุกๆ 1 รอบที่เพิ่มขึ้น ความฝืดจะเพิ่มประมาณ 3 เท่าครับ:

ผมถามเด็กๆว่าถ้าเรามีแบคทีเรียที่แบ่งเซลล์วันละครั้ง คือวันแรกมีแบคทีเรีย 1 ตัว วันที่สองกลายเป็น 2 ตัว วันที่สามกลายเป็น 4 ตัว เมื่อถึงวันที่ 30 จะมีกี่ตัว ให้เด็กๆเดา เด็กก็เดากันว่ามีเป็นร้อย เป็นพัน เป็นล้าน ผมจึงให้ลองคำนวณหรือประมาณดู เด็กๆก็นั่งคำนวณกันใหญ่ครับ สักพักก็มีเสียงตื่นเต้นว่าเป็นแสนเป็นล้านแล้ว ในที่สุดก็ได้คำตอบว่าประมาณห้าร้อยล้านครับ

ผมสอนเด็กๆคำนวณแบบประมาณด้วยจะได้เร็วๆแบบนี้ครับ เด็กๆรู้จักใช้ k (kilo-) แทนหลักพัน และ M (mega-) แทนหลักล้าน:

เด็กๆก็ตกใจกับความเร็วในการเติบโตอย่างนี้เหมือนกันครับ ผมยกตัวอย่างอีกอย่างคือเงินเฟ้อ คือราคาสินค้าจะเพิ่มขึ้นเรื่อยๆ อย่างในประเทศไทยราคาก๋วยเตี๋ยวจะเพิ่มเป็นสองเท่าทุกๆประมาณ 15-20 ปี ผมจึงให้เด็กๆไปทำเป็นการบ้านว่าราคาก๋วยเตี๋ยวเมื่อ 40 ปี และอีกประมาณ 90 ปีในข้างหน้าเป็นประมาณเท่าไรครับ

สำหรับเด็กอนุบาล 3/1 ผมสอนให้เล่นของเล่นลูกแก้วในกาละมังครับ โดยเอาลูกแก้วไปวิ่งเร็วๆตามขอบกาละมังครับ ให้สังเกตว่าเมื่อลูกแก้วหลุดออกมา มันเคลื่อนที่อย่างไร (วิ่งเป็นเส้นตรงหรือวิ่งโค้งๆ? วิ่งไปทิศทางไหน?) เล่าให้เด็กๆฟังว่าถ้าอะไรจะวิ่งเป็นวงกลมได้มันต้องถูกดึงหรือดันเข้าสู่ศูนย์กลางการหมุน ในที่นี้ขอบกาละมังทำหน้าที่ผลักลูกแก้วสู่ศูนย์กลางครับ:

สำหรับของเล่นตระกูลนี้ผมเคยรวบรวมและอธิบายไว้ในคลิปนี้ครับ: